This post demonstrates the use of Virtuoso’s SQL Transitivity Extension for performing Graph Analytics using a collection of standard algorithms.
What is a Graph?
A Graph is a pictorial — a graphic aid — for representing Entity Relationship Types, i.e., an Entity and its Characteristics.
This kind of pictorial comprises a collection of nodes and connectors that represent —
- an Entity
- an Entity Relationship Type Name (a/k/a Attribute)
- an Entity Relationship Type Value (a/k/a Value)
In the RDF Entity Relationships model, propositions are represented using sentences/statements structured as subject→predicate→object. Thus, an RDF graph comprises —
- a Subject (corresponding to the Entity, above)
- a Predicate (corresponding to the Attribute, above)
- an Object (corresponding to the Value, above)
In SQL the Table functions as the Relation, Column Names as Atrribute, and Column Values as Value via a N-Tuple representational structure.
What is a Network?
A sub-category of a Graph that depicts Entity Relationship Types that are transitive in nature i.e., all the nodes in the graph represent relatives albeit by varying degrees. Examples of popular networks include Facebook, and Twitter.
Social Network
This form of network is constructed from “knows” (as exemplified by FOAF), “friend” (as exemplified by Facebook) and “follows” (as exemplified by Twitter) connections that denote transitive entity relationship types.
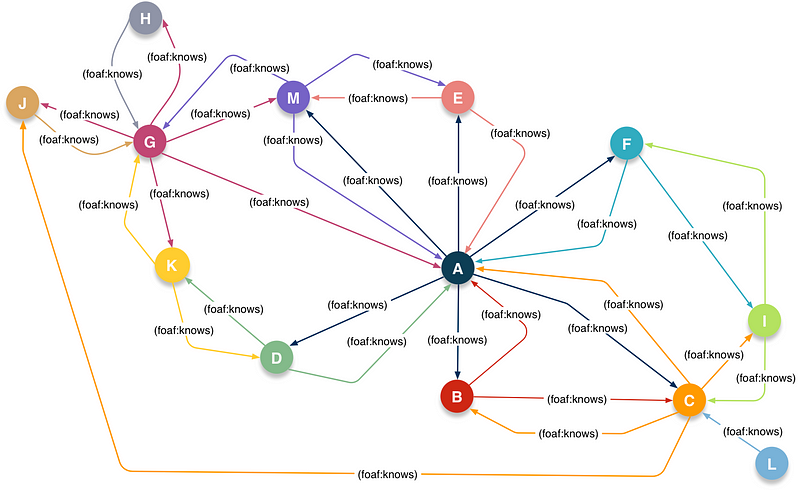
Here’s an illustration of a Social Network constructed using terms from the FOAF Vocabulary, where each foaf:knows connection denotes an instance of an owl:TranstiveProperty and owl:ObjectProperty (i.e., a Property type that has a Reference [e.g., a Hyperlink] as its value).
Friend Network
In this kind of network each :friend connection denotes a transitive relationship type that’s also symmetric in nature i.e., instance of an owl:ObjectProperty, owl:TransitiveProperty, and owl:SymmetricProperty — signified by the bidirectional arrows indicating the mutual nature of friendship.
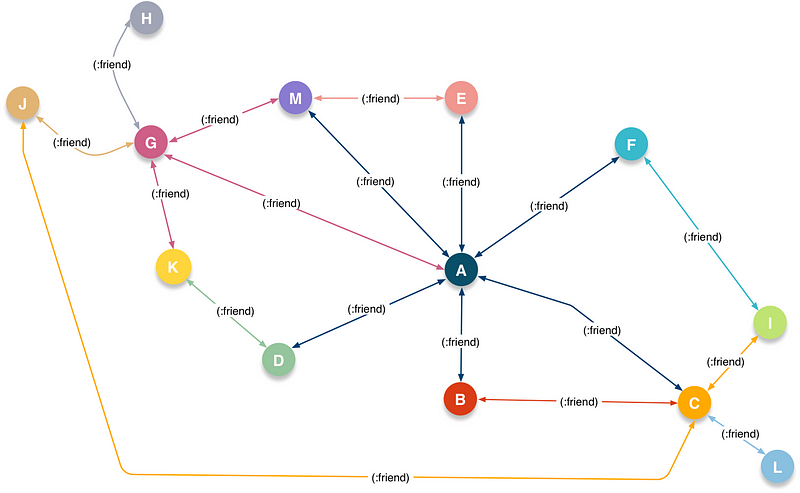
Naturally, you can use Reasoning and Inference (which underlie the notion of “Artificial Intelligence”) to generate a Friend Network from a Social Network. That will be the subject of another post in this series.
What is the difference between a Graph and a Network?
Graphs are generic Entity Relationship Type (Relations) depictions while Networks are Graphs that depict Relations that are at the very least transitive in nature i.e., nodes depict relatives by varying degrees of relatedness.
Graph Analytics
Graph Analytics are used to extract information from Entity Relationship Types as part of a query processing pipeline aimed at providing a variety of insights into the power and value of nodes within a network.
Why are Graph Analytics important?
Entity Relationships model the real world and provide a powerful basis for knowledge acquisition and dissemination, leveraging the productivity offered by computer software.
How do I apply Graph Analytics to a Knowledge Graph deployed as a Semantic Web comprising Linked Data?
This kind of Knowledge Graph is deployed as a collection of RDF sentences that adheres to Linked Data principles, meaning —
- Each Entity and Entity Relationship Type is identified unambiguously using a hyperlink (specifically, an HTTP URI)
- Entities and Entity Relationship Types are described using RDF sentence collections
Here are the steps for creating a Sociality-oriented Knowledge Graph deployed as a Semantic Web:
- Describe the Social Network — i.e., create an RDF document comprising sentences that describe the social network’s membership
- Load the RDF document to a Virtuoso instance — e.g., sponge (import) the document using our URIBurner service
- Write your queries using SPARQL-BI
- Execute your SPARQL-BI queries
- Share your Query Results pages with others via your internal network or the World Wide Web
Social Network Graph Analytics Examples
For the live examples that follow, I will be using a FOAF-based Social Network, described using RDF-Turtle Notation.
The Dataset below is loaded to a Named Graph using a SPARQL 1.1 INSERT command.
N-Tuple Representation of Data
-- FOAF Social Network for Graph Analytics
-- using SQL via Transitivity Extensions
-- Table/Relation Creation
DROP TABLE demo.foaf.knows ;
CREATE TABLE demo.foaf.knows (subject VARCHAR, object VARCHAR, PRIMARY KEY (subject, object))
ALTER INDEX foaf_knows_idx ON demo.foaf.knows PARTITION (subject VARCHAR);
CREATE INDEX foaf_knows_idx2 ON demo.foaf.knows (object, subject) PARTITION (object VARCHAR);
-- SPARQL Relation Eequivalents
-- <urn:a> foaf:knows <urn:b> , <urn:c>, <urn:d>, <urn:e>, <urn:f>, <urn:m>, <urn:g> .
INSERT INTO demo.foaf.knows VALUES ('a', 'b');
INSERT INTO demo.foaf.knows VALUES ('a', 'c');
INSERT INTO demo.foaf.knows VALUES ('a', 'd');
INSERT INTO demo.foaf.knows VALUES ('a', 'e');
INSERT INTO demo.foaf.knows VALUES ('a', 'f');
INSERT INTO demo.foaf.knows VALUES ('a', 'm');
INSERT INTO demo.foaf.knows VALUES ('a', 'g');
-- SPARQL Relation Eequivalents
-- <urn:b> foaf:knows <urn:a> , <urn:c> .
INSERT INTO demo.foaf.knows VALUES ('b', 'a');
INSERT INTO demo.foaf.knows VALUES ('b', 'c');
-- SPARQL Relation Eequivalents
-- <urn:c> foaf:knows <urn:a> , <urn:b>, <urn:i>, <urn:l> .
INSERT INTO demo.foaf.knows VALUES ('c', 'a');
INSERT INTO demo.foaf.knows VALUES ('c', 'b');
INSERT INTO demo.foaf.knows VALUES ('c', 'i');
INSERT INTO demo.foaf.knows VALUES ('c', 'l');
-- SPARQL Relation Eequivalents
-- <urn:d> foaf:knows <urn:a> , <urn:k> .
INSERT INTO demo.foaf.knows VALUES ('d', 'a');
INSERT INTO demo.foaf.knows VALUES ('d', 'k');
-- SPARQL Relation Eequivalents
-- <urn:e> foaf:knows <urn:a> , <urn:m> .
INSERT INTO demo.foaf.knows VALUES ('e', 'a');
INSERT INTO demo.foaf.knows VALUES ('e', 'm');
-- SPARQL Relation Eequivalents
-- <urn:f> foaf:knows <urn:a> , <urn:i> .
INSERT INTO demo.foaf.knows VALUES ('f', 'a');
INSERT INTO demo.foaf.knows VALUES ('f', 'i');
-- SPARQL Relation Eequivalents
-- <urn:m> foaf:knows <urn:a> , <urn:e> , <urn:g> .
INSERT INTO demo.foaf.knows VALUES ('m', 'a');
INSERT INTO demo.foaf.knows VALUES ('m', 'e');
INSERT INTO demo.foaf.knows VALUES ('m', 'g');
-- SPARQL Relation Eequivalents
-- <urn:g> foaf:knows <urn:a> , <urn:m> , <urn:k> , <urn:h> , <urn:j> .
INSERT INTO demo.foaf.knows VALUES ('g', 'a');
INSERT INTO demo.foaf.knows VALUES ('g', 'm');
INSERT INTO demo.foaf.knows VALUES ('g', 'k');
INSERT INTO demo.foaf.knows VALUES ('g', 'h');
INSERT INTO demo.foaf.knows VALUES ('g', 'j');
-- SPARQL Relation Eequivalents
-- <urn:i> foaf:knows <urn:c> , <urn:f> .
INSERT INTO demo.foaf.knows VALUES ('i', 'c');
INSERT INTO demo.foaf.knows VALUES ('i', 'f');
-- SPARQL Relation Eequivalents
-- <urn:l> foaf:knows <urn:c> .
INSERT INTO demo.foaf.knows VALUES ('l', 'c');
-- SPARQL Relation Eequivalents
-- <urn:k> foaf:knows <urn:d> , <urn:g> .
INSERT INTO demo.foaf.knows VALUES ('k', 'd');
INSERT INTO demo.foaf.knows VALUES ('k', 'g');
-- SPARQL Relation Eequivalents
-- <urn:h> foaf:knows <urn:g> .
INSERT INTO demo.foaf.knows VALUES ('h', 'g');
-- SPARQL Relation Eequivalents
-- <urn:j> foaf:knows <urn:g> .
INSERT INTO demo.foaf.knows VALUES ('j', 'g');
Graphic Representation of FOAF-based Social Network Data
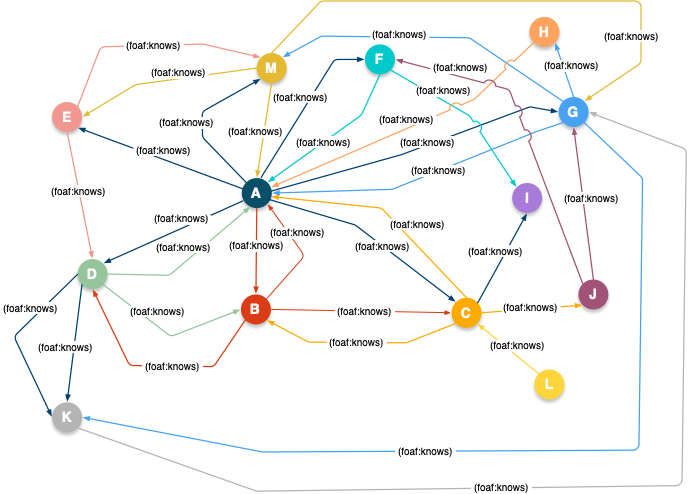
Here is a collection of demonstration queries that use SQL to implement known Graph Analytics Algorithms, courtesy of Virtuoso’s Transitivity extension.
Note:
Provide username “vdb” and password “vdb” as your authentication challenge credentials when using the live query results links that accompany each SQL Query example.
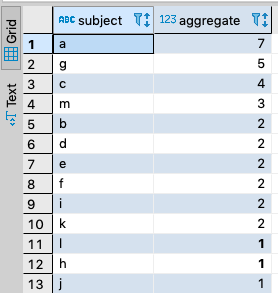
Centrality Query
Centrality measures the importance of a node in a graph simply by how “central” the node is, relative to others in the same graph.
SELECT subject, count(*)
FROM demo.foaf.knows
GROUP BY subject ORDER BY 2 DESC ;
Query Results
Live Query Results LINK.
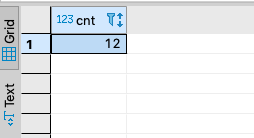
Degree Centrality Query
Measures network importance based on in-bound connections from other nodes in the graph, or out-bound connections to other nodes in the graph, given a starting node.
SELECT count(*) AS cnt
FROM (
SELECT TRANSITIVE T_DISTINCT
T_IN (1) T_OUT (2) T_MIN (1)
subject ,
object
FROM demo.foaf.knows
) AS k
WHERE k.subject = 'a' ;
Query Results
Live Query Results LINK.
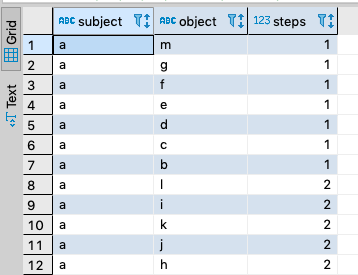
Closeness (Reach or Distance) Centrality Query
Closeness Centrality is based on the number of “hops” (sometimes counted as the number of intervening nodes plus one) between two nodes, based on the shortest path between each pair of nodes.
SELECT subject, object, sum(step) AS steps
FROM (
SELECT TRANSITIVE T_DISTINCT
T_IN (1) T_OUT (2) T_MIN (1)
subject,
object ,
T_STEP ('step_no') AS step
FROM demo.foaf.knows
) AS k
WHERE k.subject = 'a'
GROUP BY subject, object ;
Query Results
Live Query Results LINK.
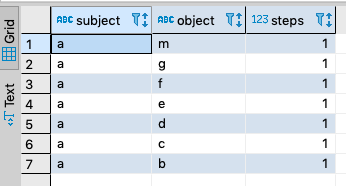
Closeness Centrality based on Shortest Path
SELECT subject, object, sum(step) AS steps
FROM (
SELECT TRANSITIVE T_DISTINCT T_SHORTEST_ONLY
T_IN (1) T_OUT (2) T_MIN (1)
subject,
object ,
T_STEP ('step_no') AS step
FROM demo.foaf.knows
) AS k
WHERE k.subject = 'a'
GROUP BY subject, object ;
Query Results
Live Query Results LINK.
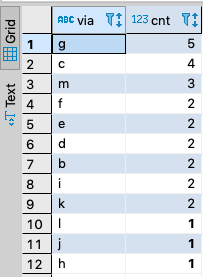
Betweenness Centrality Query
Betweenness Centrality assigns importance to a node in a network based upon the number of times that node occurs within the paths between all pairs of nodes in a graph. That is, each node in the graph is paired with every other node; the shortest path between each pair of nodes is computed; and then the number of occurrences of each intermediate node in those shortest-paths is counted, to discover their relative importance.
This is a node intermediacy metric, in a nutshell.
SELECT A.object AS via, COUNT (1) AS cnt
FROM (
SELECT TRANSITIVE T_DISTINCT T_MIN(1)
T_OUT(2) T_IN(1)
subject,
object,
T_STEP( 'step_no' ) AS dist_to_via
FROM demo.foaf.knows
) AS A
INNER JOIN (
SELECT TRANSITIVE T_DISTINCT T_SHORTEST_ONLY T_MIN(1)
T_OUT(2) T_IN(1)
subject,
object,
T_STEP( 'step_no' ) AS dist_from_via
FROM demo.foaf.knows
) AS B
ON (A.object = B.subject)
WHERE A.subject = 'a'
GROUP BY A.object
ORDER BY 2 DESC ;
Query Results
Live Query Results LINK.
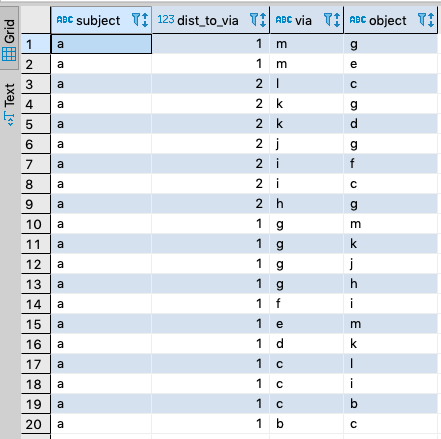
Betweenness Centrality using Shortest Path
In this metric the shortest path is explicitly sought when determining the intermediacy metric.
SELECT A.subject, A.dist_to_via, A.object AS via, B.object
FROM (
SELECT TRANSITIVE T_DISTINCT T_MIN(1)
T_OUT(2) T_IN(1)
subject,
object,
T_STEP( 'step_no' ) AS dist_to_via
FROM demo.foaf.knows
) AS A
INNER JOIN (
SELECT TRANSITIVE T_DISTINCT T_SHORTEST_ONLY T_MIN(1)
T_OUT(2) T_IN(1)
subject,
object,
T_STEP( 'step_no' ) AS dist_from_via
FROM demo.foaf.knows
) AS B
ON (A.object = B.subject)
WHERE A.subject = 'a'
AND B.object <> 'a'
-- GROUP BY A.subject, A.dist_to_via, A.object, B.object
ORDER BY 3 DESC ;
Query Results
Live Query Results LINK.
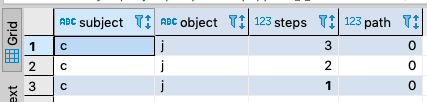
Betweenness Centrality using out-link threshold via T_MAX()
In this intermediacy metric calculation with the focus on out-bound rather than in-bound links, with any shortest path option.
SELECT subject, object, step AS steps, path
FROM (
SELECT TRANSITIVE T_DISTINCT
T_IN (1) T_OUT (2) T_MIN (1)
subject,
object ,
T_STEP ('step_no') AS step,
T_STEP ('path_id') AS path
FROM demo.foaf.knows
) AS k
WHERE k.subject = 'c' AND k.object = 'j'
-- GROUP BY subject, object ;
ORDER BY steps DESC ;
Query Results
Live Query Results LINK.
Conclusion
Contrary to general misconceptions about the capabilities of the SQL (an open standard), you can extend it using Stored Procedures with regards to adding new functionality such as Transitivity for performing Graph Analytics using a variety of common algorithms. Even better, you can do so in a manner that preserves your ability to mix and match “best of class” products that exploit SQL via ODBC, JDBC, ADO.NET, or OLE DB.
Related
-
Free Evaluation and Download Page — for Windows, Linux, and macOS
-
Virtuoso Pay-As-You-Go (PAGO) Edition from Amazon Web Services (AWS) Cloud